www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Limit ›
Tentukan \(a\) dan \(b\) sehingga
\[ \displaystyle{ \lim_{x\to 0} \frac{a+\cos{(bx)}}{x^2} = -2} \]
Pembahasan:
Pertama, \(\displaystyle{ \lim_{x\to 0} a+\cos{(bx)} } \) haruslah bernilai 0. Sebab jika hal ini tidak terjadi (katakanlah \(\displaystyle{ \lim_{x\to 0} a+\cos{(bx)} = c \neq 0 } \) ) akan berakibat
\[ \lim_{x\to 0} \frac{a+\cos{(bx)}}{x^2} = \frac{c}{ \displaystyle \lim_{x\to 0} x^2} = \infty \]
yang bertentangan dengan pernyataan
\[ \lim_{x\to 0} \frac{a+\cos{(bx)}}{x^2} = -2 \]
Dengan demikian, kita peroleh
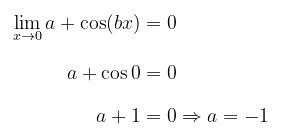
Kemudian karena \(\displaystyle{ \lim_{x\to 0} \frac{a+\cos{(bx)}}{x^2} } \) berbentuk \( \frac{0}{0} \) untuk \(a = -1\), maka kita dapat menerapkan dalil I’Hopital yakni
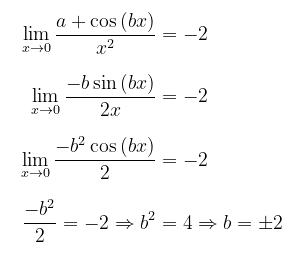
Jadi, nilai \(b\) adalah \(±2\).